SISTEMAS DE
REESCRITURA

“Las reglas de reescritura son una forma simple y natural de describir cualquier clase de proceso no numérico” (J.A. Gognen)

“Pero solamente debe llamarse ‘interpretación’ a esto: sustituir una expresión de la regla por otra” (Wittgenstein. Investigaciones Filosóficas)


Definición

Un Sistema de Reescritura se compone de:
  1. Un conjunto de reglas (llamadas reglas de reescritura”), cuya forma general es:


    Abreviadamente, “p → q si c”, siendo p y q expresiones en general. Se puede leer como “p se reescribe como q” o “p se sustituye por q” o “p se reduce a q”, todas ellas bajo la condición c.

    La flecha indica “sustitución”. Si la condición no existe, se tiene lo que se suele denominar “ecuación directa”, pero es mejor denominarla “sustitución pura” o “sustitución incondicional”.

  2. Un algoritmo o programa de control que realiza dos tareas. Primero, el análisis de cada regla para determinar si es aplicable. Segundo, cuando una regla es aplicable, realiza el proceso de sustitución en la expresión la parte izquierda de la regla por la parte derecha.

  3. Un contexto. El contexto de un Sistema de Reescritura es el entorno sobre el que se van a realizar las sustituciones. Pueden ser números, funciones, expresiones algebraicas, etc.

Reducción

El proceso de sustitución de una expresión que aparece en el lado izquierdo de una regla de reescritura por sus correspondiente lado derecho se denomina reducción. De tal forma que la evaluación de una expresión implica una secuencia de reducciones.

Si de a se deriva directamente b (a se reduce a b en un solo paso), se escribe a ⇒ b. Si de a se deriva b a través de varios pasos, se simboliza por a ⇒* b.

A partir de una expresión inicial a1, aplicando las reglas, se obtiene una secuencia de reducciones: Cada paso discreto, de ai a ai+1 es una reducción. El último término, que no puede reducirse más se dice que está en “forma normal” y que la expresión es “residual”.

El término “reducción”, no obstante, es equívoco, pues puede ocurrir que ai+1 sea más grande que ai. Es más general usar el término “transformación” o “reescritura”.


Ejemplos
  1. En el contexto de las potencias del tipo xn, tenemos las tres reglas siguientes:


    Ejemplo:

    x5 ⇒ x × x4 ⇒ x × (x2 × x2) ⇒ x × ((x × x) × (x × x))

    Se han aplicado sucesivamente las reglas 3, 2 y 2.

  2. El ejemplo más conocido de Sistema de Reescritura es el cálculo lambda. El contexto es el de las funciones lambda, junto con sus argumentos. La regla general consiste en sustituir los parámetros (identificados por el prefijo “λ” por los argumentos. Por ejemplo:


  3. El sistema definido por las sustituciones directas


    permiten representar todas las funciones computables y es la base los Combinadores Funcionales [ver Adenda].

Propiedades

Las dos propiedades más importantes de un Sistema de Reescritura son:
  1. Confluencia ( o propiedad de Church-Rosser).
    Si existe más de una regla que puede aplicarse en cada punto del proceso, hay que considerar el orden o el criterio de selección de la regla a aplicar por parte del programa de control.


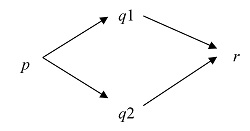
    Un conjunto de reglas en las que el orden de aplicación de dichas reglas es indiferente se dice que es Church-Rosser. Esto significa que si existen dos reducciones del mismo término p a dos términos diferentes, q1 y q2, podemos encontrar otras dos reducciones desde estos términos hasta un mismo término r. La unicidad implica que el orden de aplicación de las reglas es indiferente.

  2. Normalización.
    El proceso de aplicación de las reglas de reescritura puede terminar o no. Si realmente se alcanza un final (es decir, no se produce una secuencia infinita de reducciones), el conjunto de reglas se dice que es de terminación finita. Y todas las expresiones pueden alcanzar la forma normal.
Un Sistema de Reescritura que tenga estas dos propiedades (confluencia y normalización) se denomina “completo”.


Sistemas de Reescritura concretos y abstractos

Los Sistemas de Reescritura concretos son los que tienen una semántica definida a priori. En los Sistemas de Reescritura abstractos la semántica es libre, es decir, admiten muchas interpretaciones, llamadas “modelos”, como ocurre en el caso de los sistemas axiomáticos formales.

Muchos problemas o dominios, aparentemente diferentes, aparecen con una estructura formal análoga contemplados desde el paradigma de los Sistemas de Reescritura. De hecho, existen los llamados “Sistemas de Reducción Abstractos” (Abstract Reduction Systems, ARS), pues muchos aspectos de la reescritura se pueden estudiar independientemente de la naturaleza o semántica de los objetos.


Especificación en MENTAL

Forma general de una regla y proceso de evaluación

En MENTAL, una regla de reescritura se codifica mediante una expresión genérica, parametrizada o no: Al ser las reglas expresiones genéricas, se aplican automáticamente en todo momento por parte del intérprete de MENTAL, por lo que no es necesario un programa de control específico. Una expresión dada se autoevalúa si no puede aplicarse ninguna regla, o se evalúa a otra expresión como consecuencia del proceso de evaluación automático.


Las posibilidades de MENTAL como Sistema de Reescritura

MENTAL proporciona un modelo computacional completo, un marco genérico y flexible para definir sistemas de reescritura. He aquí algunas de sus posibilidades en este sentido:
Ejemplos
  1. El ejemplo 1 anterior se codificaría así:

    ⟨( (x^n = 1) ← n=0 )⟩

    ⟨( (x^n = (x^(n÷2) * x^(n÷2)) ) ← (n = (n÷2)*2) )⟩

    ⟨( (x^n = (x * x^(n−1)) ) ← n≠0 ← (n ≠ n÷2)*2) )⟩

    X^5 // ev. (x * x^4) ev. (x * x^2 * x^2) ev. (x*x*x*x*x)

    Las 3 reglas realmente se podían codificar como una sola, con las condiciones jerarquizadas.

  2. Un ejemplo basado en funciones:

    ⟨( (f(x y) = (g(x+y) g(x*y)) )⟩ // no hay condición
    ⟨( (g(x) = 24) ← x>10 )⟩
    ⟨( (g(x) = 12) ← x≤10 )⟩

    f(3 4) // ev. (g(7) g(12)) ev. (12 24)
    f(1 1) // ev. (g(2) g(1)) ev. (12 12)

Adenda

Orígen

Los Sistemas de Reescritura surgieron históricamente del cálculo lambda y de la lógica combinatoria. Están desempeñando un importante papel como modelo teórico de computación, principalmente en el área de los lenguajes funcionales. Sus principales atractivos son su carácter genérico y su simplicidad.

Los Sistemas de Reescritura constituyen un formalismo de programación totalmente genérico que sirve para especificar cualquier función computable, como han demostrado Bergstra y Tucker [1985]. Pero al basarse solo en dos primitivas conceptuales (la sustitución y la condición), impide que se convierta en un lenguaje universal.

Según Gognen [1984], “las reglas de reescritura constituyen una forma simple y natural de describir cualquier clase de proceso no numérico”.


Relaciones con otros dominios y aplicaciones Otras aplicaciones de los Sistemas de Reescritura son: especificación algebraica, teoría de la recursión, demostración automática de teoremas, transformación de programas, verificación de programas, traducción automática, compiladores, proceso del lenguaje natural, teoría de autómatas, proceso de señales, sistemas evolutivos, etc.


Lenguaje OBJ

OBJ [Gognen, 1979] es un lenguaje de muy alto nivel que se basa en reglas de reescritura, que se llaman “ecuaciones lógicas” y el sistema lógico correspondiente se denomina “lógica ecuacional”.

En OBJ la forma sintáctica de una regla de reescritura es Una característica interesante de OBJ es su sintaxis flexible en la que es posible definir operaciones prefijas, postfijas, infijas y mixfijas. Las operaciones mixfijas son las más generales. El término “mixfija” se debe a P. Mosses (también se usa la palabra “distfija”, en la que “dist” indica distribuida) y se refiere a la posibilidad de especificar operandos mezclados con símbolos u otras palabras. Por ejemplo, IF_THEN_ELSE_FI es la declaración mixfija correspondiente a “condicional”, en donde los guiones bajos corresponden a los operandos.


Combinadores funcionales

Los combinadores funcionales tienen su origen en dos ideas principales: La idea de eliminar variables en las funciones tiene su origen en las ideas de Moses Schönfinkel, que en los 1920s desarrolló el llamado “cálculo funcional”.

Curry desarrolló la misma idea, independientemente, bajo el nombre de “lógica combinatoria” [Curry, 1958, 1971].

Por ejemplo, si tenemos las funciones y definimos la función entonces F se puede expresar como La asociatividad se supone a la derecha, es decir, Si definimos una nueva función en donde los argumentos pueden representar funciones, se tiene que Por lo tanto, F = QAM es una nueva función que puede definirse a partir de las funciones Q, A y M, desapareciendo las variables en su definición y expresándose sólo mediante otras funciones.

Schönfinkel descubrió que era suficiente con introducir dos formas combinatorias (combinadores) primitivas para expresar cualquier función, sin necesidad de variables: La primera se puede considerar la distribución de z sobre x e y.

La segunda es la reducción o eliminación del segundo argumento o la proyección sobre el primer argumento.

Por ejemplo, la función identidad Ix = x es una función derivada, pues se puede expresar mediante las dos primitivas: I = SKK

En efecto,
Bibliografía